Les arbres binaires

2.Arbre binaire

Un arbre binaire est un arbre non  vide  formé d’un nœud, sa racine, et de deux sous-arbres binaires, l’un appelé le fils gauche, l’autre le fils droit. Chaque nœud porte une information, appelée son contenu. Un arbre non vide est donc entièrement décrit par le triplet (contenu de la racine ( information),fils gauche,  fils droit). Il suffit de préciser le type du contenu d’un nœud. 

                                                                                                                fig2 : arbre binaire

2-1 représentation des arbres binaires :

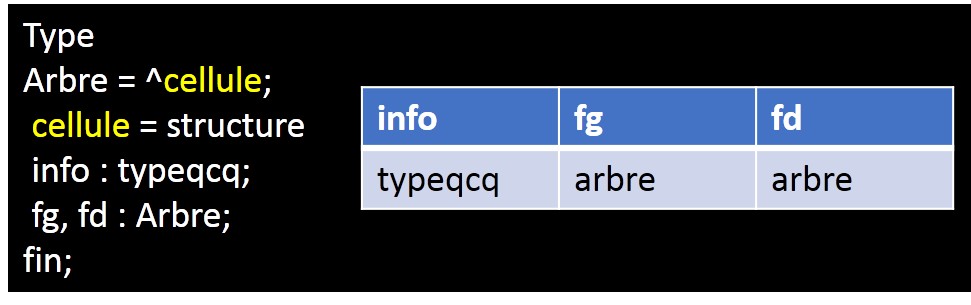
Exemple : l'arbre suivant :

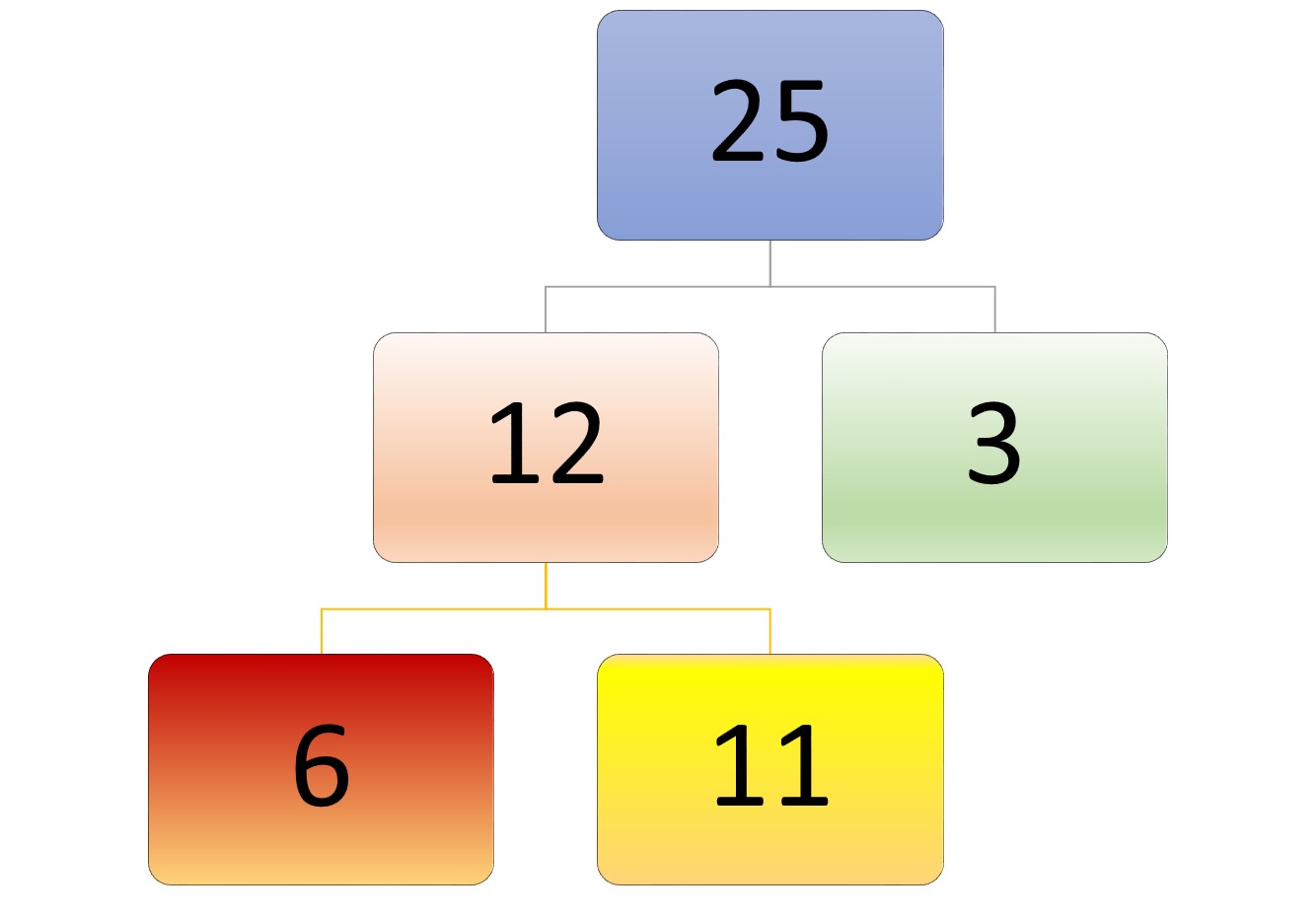
est représenté comme :

2-2 parcours d'arbre binaire :

le Parcours d'un arbre c'est l'action qui permettre de visiter  visiter tous ses nœuds. Il existe différentes façons de le faire, cela dépend de l’ordre de passage par les noeuds.

2.2.1 parcours infixé 

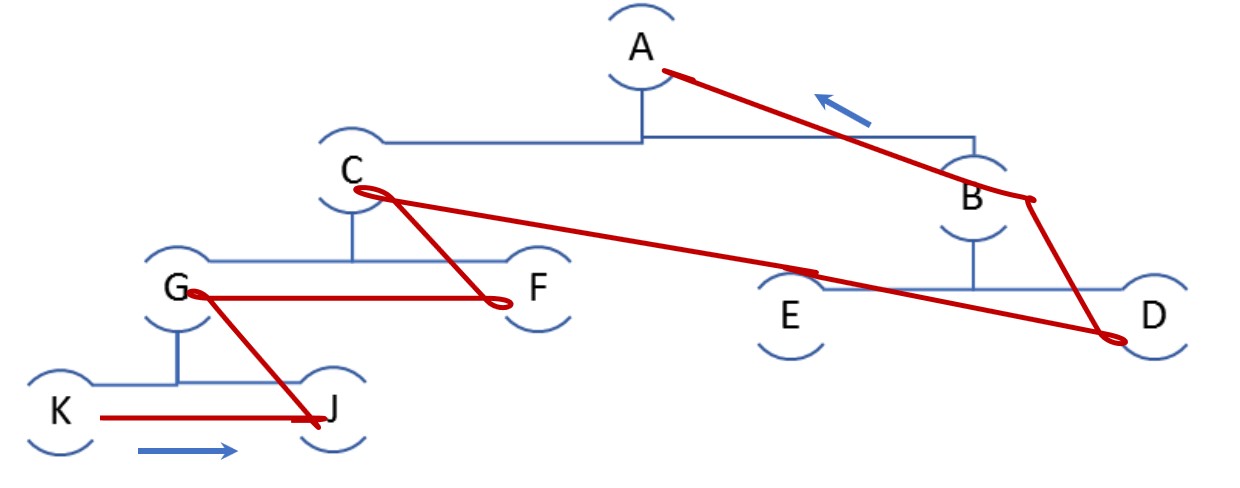
exemple : le parcours infixé de l'arbre de la figure fig2 donne : K G J C F A E B D

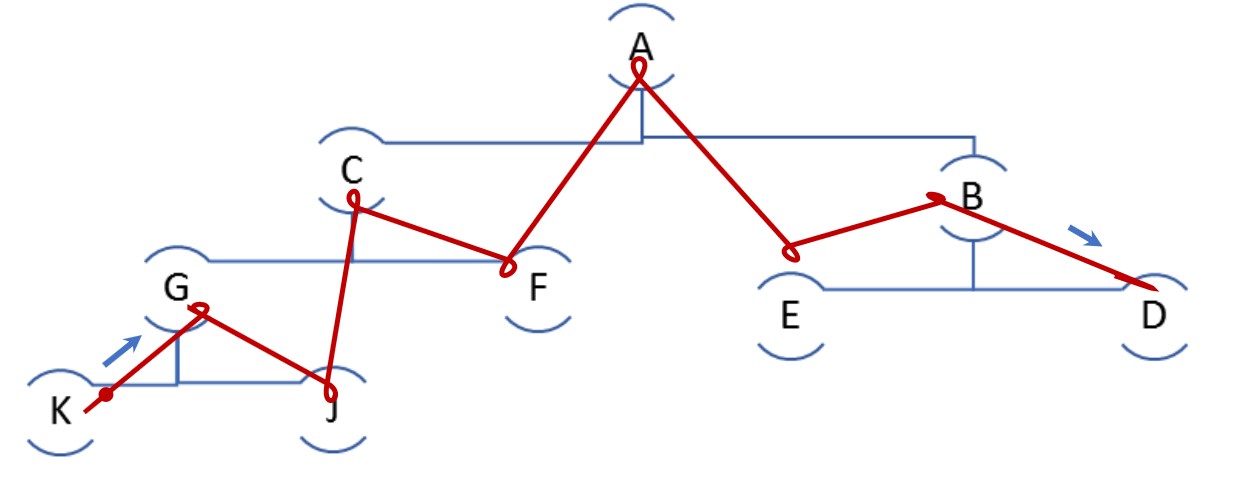
2.2.2 parcours préfixé 

exemple :

le parcours préfixé de l'arbre de la fig2 donne :  A C G K J F B E D

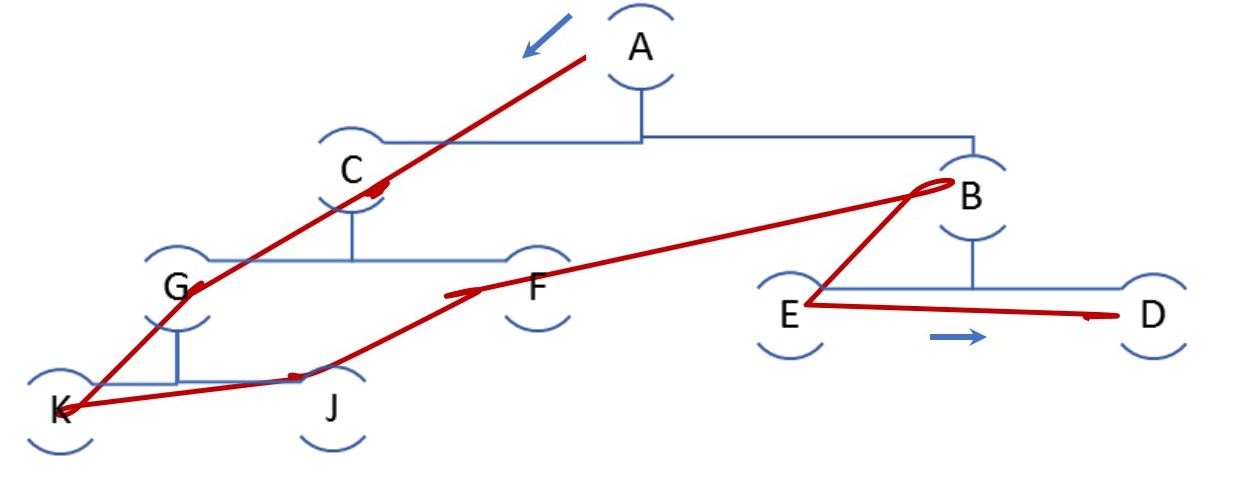
2.2.3 parcours postfixé 

exemple :

le parcours postfixé de l'arbre fig2 donne : K J G F C E D B A

2-3 Hauteur d'un arbre binaire :
La hauteur d'un arbre binaire est le nombre des nœuds parcourus sur le plus long chemin possible depuis la racine.


fonction max(a,b:entier):entier
debut
si a>b alors retourner a
           sinon retourner b
fin;

2.4 calcul de la taille d'un arbre binaire
Pour calculer la taille d’un arbre, il faut là encore parcourir toutes ses branches et compter les nœuds. 


2.5 Nombre des feuilles d'un arbre binaires: