introduction aux graphes
1-Introduction
Un graphe est une structure qui permet de représenter plusieurs situations réelles, en but de leur apporter des solutions mathématiques et informatique, tel que :
– Les réseaux de transport (routiers, ferrés, aériens ·· · ),
– Les réseaux téléphoniques, électriques, de gaz,·· · etc,
– Les réseaux d’ordinateurs,
2. Notion de graphe:
Un graphe est défini par un couple (S, A) où S est un ensemble de sommets (nœuds ou points) et A est un sous ensemble du produit cartésien (S ⇥ S) représentant les relations existant entre les sommets.
Exemple : S = 1, 2, 3, 4, 5
A = (1, 2), (1, 4), (2, 5)(3, 5), (3, 6), (4, 2), (5, 4), (6, 6)
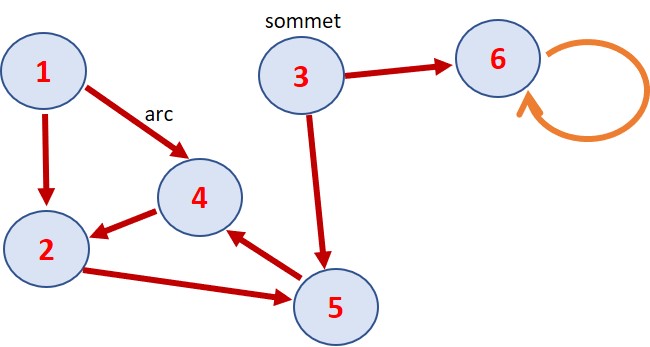
3.1 Graphe orienté
C’est un graphe où les relations
entre les sommets
sont définies dans un seul sens . Dans
ce cas les relations sont appelées
"arcs".
3.2 Graphe non orienté
C’est un graphe où les relations sont définies dans les deux sens. Dans ce cas, les relations sont appelées "arêtes".

3.3 Graphe étiqueté ( pondéré)
C’est un graphe orienté ou non où à chaque arc ou arête correspond une valeur ou une étiquette représentant son coût (ou distance).

4.Notions sur les graphes
4.1 Origine et extrémité
Si a = (D, F) est un arc de D vers F alors :
– D est l’origine de a et F est son extrémité
– D est un prédécesseur de F et F est un successeur de D
Si l’origine et l’extrémité d’un arc se coïncident on l’appelle une boucle (6,6).
4.2 Chemin
Un chemin est un ensemble d’arcs a1, a2, ·· · , ap où Origine(ai+1) = Extrémité(ai),
Le chemin est de longueur p - 1
Exemple : {(1, 2), (2, 5), (5, 4)}
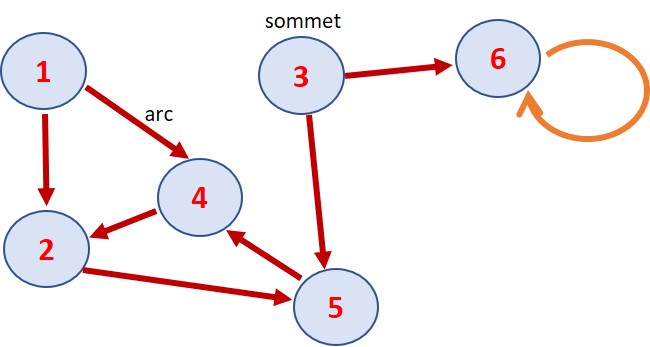
4.2 Circuit
Un circuit est un chemin a1, a2, ·· · , ap où Origine(a1) = Extrémité(ap)
Exemple : {(2, 5), (5, 4), (4, 2)}

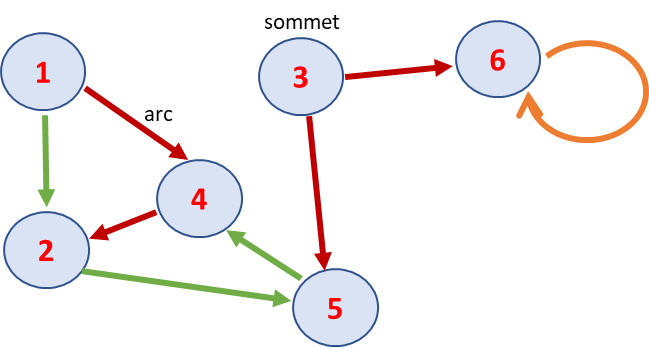
4.3 Chaine
Une chaine est un chemin non orienté.
Exemple : {(1, 4), (5, 4), (3, 5)}
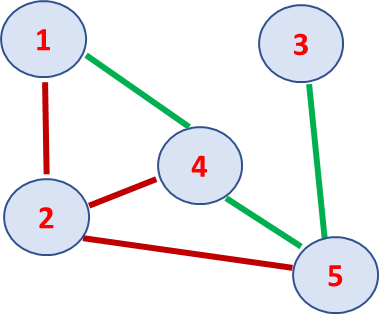
Un cycle est une chaîne fermée.
Exemple : {(1, 2), (2, 5), (5, 4), (1, 4)}

