Parcours des graphes
Parcours des graphes
De même que pour les arbres, il est important de pouvoir parcourir un graphe selon certaines règles, cependant, le parcours des graphe est un peut différent de celui des arbres. Dans un arbre, si on commence à partir de la racine on peut atteindre tous les nœuds, malheureusement, ce n’est pas le cas pour un graphe où on est obligé de reprendre le parcours tant qu’il y a des sommets non visités. En plus un graphe peut contenir des cycles, ce qui conduit à des boucles infinies de parcours.
Il existe deux types de parcours de graphes : le parcours en profondeur d’abord (Depth First Search) et le parcours en largeur d’abord (Breadth First Search).
1.Parcours en profondeur d'abord
Le principe du DFS est de visiter
tous les sommets
en allant le plus profondément possible dans le graphe.

L'application de cette procédure sur le graphe G1 donne :
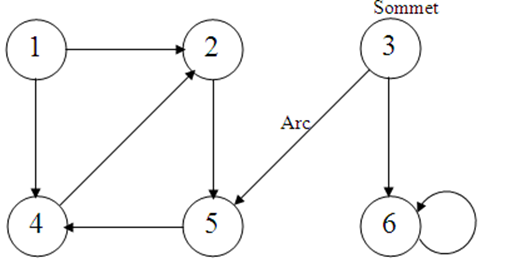
Graphe G1
1 2 5 4 3 6
2.Parcours en largeur d'abord
Dans ce parcours, un sommet s est fixé comme origine et l’on visite tous les sommet situés à une distance k de s avant de passer à ceux situés à k + 1. On utilise pour cela une file d’attente.

le parcours du graphe G1 donne:
1 2 4 5 3 6
